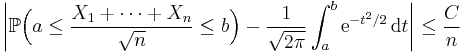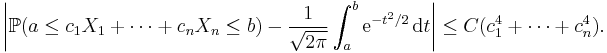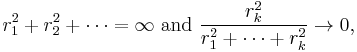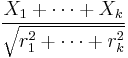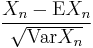Central limit theorem
In probability theory, the central limit theorem (CLT) states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed (Rice 1995). The central limit theorem also requires the random variables to be identically distributed, unless certain conditions are met. Since real-world quantities are often the balanced sum of many unobserved random events, this theorem provides a partial explanation for the prevalence of the normal probability distribution. The CLT also justifies the approximation of large-sample statistics to the normal distribution in controlled experiments.
A simple example of the central limit theorem is given by the problem of rolling a large number of dice, each of which is weighted unfairly in some unknown way. The distribution of the sum (or average) of the rolled numbers will be well approximated by a normal distribution, the parameters of which can be determined empirically.
For other generalizations for finite variance which do not require identical distribution, see Lindeberg's condition, Lyapunov's condition, Gnedenko and Kolmogorov states.
In more general probability theory, a central limit theorem is any of a set of weak-convergence theories. They all express the fact that a sum of many independent random variables will tend to be distributed according to one of a small set of "attractor" (i.e. stable) distributions. Specifically, the sum of a number of random variables with power law tail distributions decreasing as 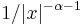 where
where 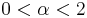 (and therefore having infinite variance) will tend to a stable distribution with stability parameter (or index of stability) of
(and therefore having infinite variance) will tend to a stable distribution with stability parameter (or index of stability) of 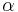 as the number of variables grows.[1] This article is concerned only with the classical (i.e. finite variance) central limit theorem.
as the number of variables grows.[1] This article is concerned only with the classical (i.e. finite variance) central limit theorem.
Contents |
Classical central limit theorem

The central limit theorem is also known as the second fundamental theorem of probability. (The Law of large numbers is the first.)
Let X1, X2, X3, …, Xn be a sequence of n independent and identically distributed (iid) random variables each having finite values of expectation µ and variance σ2 > 0. The central limit theorem states that as the sample size n increases the distribution of the sample average of these random variables approaches the normal distribution with a mean µ and variance σ2/n irrespective of the shape of the common distribution of the individual terms Xi.
For a more precise statement of the theorem, let Sn be the sum of the n random variables, given by
Then, if we define new random variables
then they will converge in distribution to the standard normal distribution N(0,1) as n approaches infinity. N(0,1) is thus the asymptotic distribution of the Zn's. This is often written as
Zn can also be expressed as
where
is the sample mean.
Convergence in distribution means that, if Φ(z) is the cumulative distribution function of N(0,1), then for every real number z, we have
or
Proof
For a theorem of such fundamental importance to statistics and applied probability, the central limit theorem has a remarkably simple proof using characteristic functions. It is similar to the proof of a (weak) law of large numbers. For any random variable, Y, with zero mean and unit variance (var(Y) = 1), the characteristic function of Y is, by Taylor's theorem,
where o (t2 ) is "little o notation" for some function of t that goes to zero more rapidly than t2. Letting Yi be (Xi − μ)/σ, the standardized value of Xi, it is easy to see that the standardized mean of the observations X1, X2, ..., Xn is
By simple properties of characteristic functions, the characteristic function of Zn is
But this limit is just the characteristic function of a standard normal distribution N(0, 1), and the central limit theorem follows from the Lévy continuity theorem, which confirms that the convergence of characteristic functions implies convergence in distribution.
Convergence to the limit
The central limit theorem gives only an asymptotic distribution. As an approximation for a finite number of observations, it provides a reasonable approximation only when close to the peak of the normal distribution; it requires a very large number of observations to stretch into the tails.
If the third central moment E((X1 − μ)3) exists and is finite, then the above convergence is uniform and the speed of convergence is at least on the order of 1/n1/2 (see Berry-Esseen theorem).
The convergence to the normal distribution is monotonic, in the sense that the entropy of Zn increases monotonically to that of the normal distribution, as proven in Artstein, Ball, Barthe and Naor (2004).
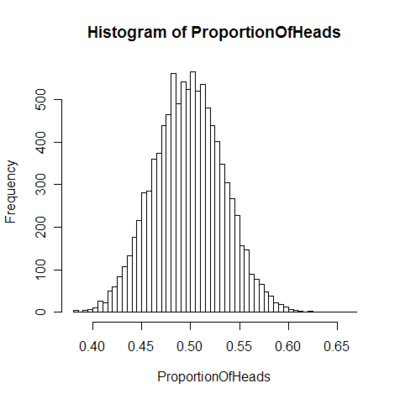
The central limit theorem applies in particular to sums of independent and identically distributed discrete random variables. A sum of discrete random variables is still a discrete random variable, so that we are confronted with a sequence of discrete random variables whose cumulative probability distribution function converges towards a cumulative probability distribution function corresponding to a continuous variable (namely that of the normal distribution). This means that if we build a histogram of the realisations of the sum of n independent identical discrete variables, the curve that joins the centers of the upper faces of the rectangles forming the histogram converges toward a Gaussian curve as n approaches infinity. The binomial distribution article details such an application of the central limit theorem in the simple case of a discrete variable taking only two possible values.
Relation to the law of large numbers
The law of large numbers as well as the central limit theorem are partial solutions to a general problem: "What is the limiting behavior of Sn as n approaches infinity?" In mathematical analysis, asymptotic series are one of the most popular tools employed to approach such questions.
Suppose we have an asymptotic expansion of ƒ(n):
Dividing both parts by φ1(n) and taking the limit will produce a1, the coefficient of the highest-order term in the expansion, which represents the rate at which ƒ(n) changes in its leading term.
Informally, one can say: "ƒ(n) grows approximately as a1 φ(n)". Taking the difference between ƒ(n) and its approximation and then dividing by the next term in the expansion, we arrive at a more refined statement about ƒ(n):
Here one can say that the difference between the function and its approximation grows approximately as a2 φ2(n). The idea is that dividing the function by appropriate normalizing functions, and looking at the limiting behavior of the result, can tell us much about the limiting behavior of the original function itself.
Informally, something along these lines is happening when the sum, Sn, of independent identically distributed random variables, X1, ..., Xn, is studied in classical probability theory. If each Xi has finite mean μ, then by the Law of Large Numbers, Sn/n → μ.[2] If in addition each Xi has finite variance σ2, then by the Central Limit Theorem,
where 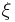 is distributed as N(0, σ2). This provides values of the first two constants in the informal expansion
is distributed as N(0, σ2). This provides values of the first two constants in the informal expansion
In the case where the Xi's do not have finite mean or variance, convergence of the shifted and rescaled sum can also occur with different centering and scaling factors:
or informally
Distributions 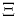 which can arise in this way are called stable.[3] Clearly, the normal distribution is stable, but there are also other stable distributions, such as the Cauchy distribution, for which the mean or variance are not defined. The scaling factor bn may be proportional to nc, for any c ≥ 1/2; it may also be multiplied by a slowly varying function of n.[4][5]
which can arise in this way are called stable.[3] Clearly, the normal distribution is stable, but there are also other stable distributions, such as the Cauchy distribution, for which the mean or variance are not defined. The scaling factor bn may be proportional to nc, for any c ≥ 1/2; it may also be multiplied by a slowly varying function of n.[4][5]
The Law of the Iterated Logarithm tells us what is happening "in between" the Law of Large Numbers and the Central Limit Theorem. Specifically it says that the normalizing function 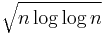 intermediate in size between n of The Law of Large Numbers and √n of the central limit theorem provides a non-trivial limiting behavior.
intermediate in size between n of The Law of Large Numbers and √n of the central limit theorem provides a non-trivial limiting behavior.
Illustration
Given its importance to statistics, a number of papers and computer packages are available that demonstrate the convergence involved in the central limit theorem. [6]
Alternative statements of the theorem
Density functions
The density of the sum of two or more independent variables is the convolution of their densities (if these densities exist). Thus the central limit theorem can be interpreted as a statement about the properties of density functions under convolution: the convolution of a number of density functions tends to the normal density as the number of density functions increases without bound, under the conditions stated above.
Characteristic functions
Since the characteristic function of a convolution is the product of the characteristic functions of the densities involved, the central limit theorem has yet another restatement: the product of the characteristic functions of a number of density functions becomes close to the characteristic function of the normal density as the number of density functions increases without bound, under the conditions stated above. However, to state this more precisely, an appropriate scaling factor needs to be applied to the argument of the characteristic function.
An equivalent statement can be made about Fourier transforms, since the characteristic function is essentially a Fourier transform.
Extensions to the theorem
Multidimensional central limit theorem
We can easily extend proofs using characteristic functions for cases where each individual Xi is an independent and identically distributed random vector, with mean vector μ and covariance matrix Σ (amongst the individual components of the vector). Now, if we take the summations of these vectors as being done componentwise, then the Multidimensional central limit theorem states that when scaled, these converge to a multivariate normal distribution.
Products of positive random variables
The logarithm of a product is simply the sum of the logarithms of the factors. Therefore when the logarithm of a product of random variables that take only positive values approaches a normal distribution, the product itself approaches a log-normal distribution. Many physical quantities (especially mass or length, which are a matter of scale and cannot be negative) are the products of different random factors, so they follow a log-normal distribution.
Whereas the central limit theorem for sums of random variables requires the condition of finite variance, the corresponding theorem for products requires the corresponding condition that the density function be square-integrable (see Rempala 2002).
Lack of identical distribution
The central limit theorem also applies in the case of sequences that are not identically distributed, provided one of a number of conditions apply.
Lyapunov condition
Let Xn be a sequence of independent random variables defined on the same probability space. Assume that Xn has finite expected value μn and finite standard deviation σn. We define
If for some  , the expected values
, the expected values ![\mathbb{E}\left[|X_{i}|^{2+\delta}\right]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/386e20c2c2cf9d311f8f22e4bf877848.png) are finite for every
are finite for every 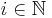 and the Lyapunov's condition
and the Lyapunov's condition
is satisfied, then the distribution of the random variable
converges to the standard normal distribution N(0, 1).
Lindeberg condition
In the same setting and with the same notation as above, we can replace the Lyapunov condition with the following weaker one (from Lindeberg in 1920). For every ε > 0
where 1{…} is the indicator function. Then the distribution of the standardized sum Zn converges towards the standard normal distribution N(0,1).
Beyond the classical framework
Asymptotic normality, that is, convergence to the normal distribution after appropriate shift and rescaling, is a phenomenon much more general than the classical framework treated above, namely, sums of independent random variables (or vectors). New frameworks are revealed from time to time; no single unifying framework is available for now.
Under weak dependence
A useful generalization of a sequence of independent, identically distributed random variables is a mixing random process in discrete time; "mixing" means, roughly, that random variables temporally far apart from one another are nearly independent. Several kinds of mixing are used in ergodic theory and probability theory. See especially strong mixing (also called α-mixing) defined by 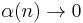 where
where 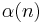 is so-called strong mixing coefficient.
is so-called strong mixing coefficient.
A simplified formulation of the central limit theorem under strong mixing is given in (Billingsley 1995, Theorem 27.4):
Theorem. Suppose that 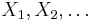 is stationary and α-mixing with
is stationary and α-mixing with 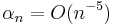 and that
and that 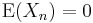 and
and 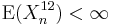 . Denote
. Denote 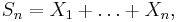 then the limit
then the limit 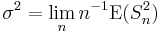 exists, and if
exists, and if 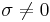 then
then 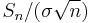 converges in distribution to
converges in distribution to 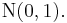
In fact, 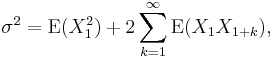 where the series converges absolutely.
where the series converges absolutely.
The assumption 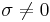 cannot be omitted, since the asymptotic normality fails for
cannot be omitted, since the asymptotic normality fails for 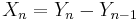 where
where 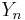 are another stationary sequence.
are another stationary sequence.
For the theorem in full strength see (Durrett 1996, Sect. 7.7(c), Theorem (7.8)); the assumption 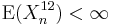 is replaced with
is replaced with 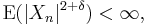 and the assumption
and the assumption 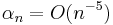 is replaced with
is replaced with 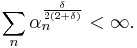 Existence of such
Existence of such  ensures the conclusion. For encyclopedic treatment of limit theorems under mixing conditions see (Bradley 2005).
ensures the conclusion. For encyclopedic treatment of limit theorems under mixing conditions see (Bradley 2005).
Martingale central limit theorem
Theorem. Let a martingale 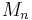 satisfy
satisfy
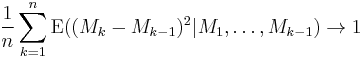 in probability as n tends to infinity,
in probability as n tends to infinity,- for every
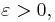
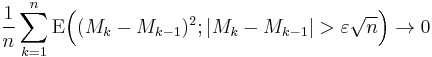 as n tends to infinity,
as n tends to infinity,
then 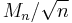 converges in distribution to N(0,1) as n tends to infinity.
converges in distribution to N(0,1) as n tends to infinity.
See (Durrett 1996, Sect. 7.7, Theorem (7.4)) or (Billingsley 1995, Theorem 35.12).
Caution: The restricted expectation 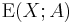 should not be confused with the conditional expectation
should not be confused with the conditional expectation 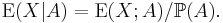
Convex bodies
Theorem (Klartag 2007, Theorem 1.2). There exists a sequence  for which the following holds. Let
for which the following holds. Let  , and let random variables
, and let random variables  have a log-concave joint density f such that
have a log-concave joint density f such that 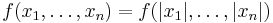 for all
for all 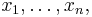 and
and 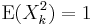 for all
for all 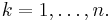 Then the distribution of
Then the distribution of 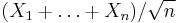 is
is 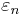 -close to
-close to 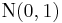 in the total variation distance.
in the total variation distance.
These two  -close distributions have densities (in fact, log-concave densities), thus, the total variance distance between them is the integral of the absolute value of the difference between the densities. Convergence in total variation is stronger than weak convergence.
-close distributions have densities (in fact, log-concave densities), thus, the total variance distance between them is the integral of the absolute value of the difference between the densities. Convergence in total variation is stronger than weak convergence.
An important example of a log-concave density is a function constant inside a given convex body and vanishing outside; it corresponds to the uniform distribution on the convex body, which explains the term "central limit theorem for convex bodies".
Another example: 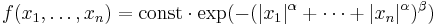 where
where  and
and 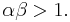 If
If 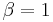 then
then  factorizes into
factorizes into 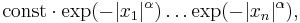 which means independence of
which means independence of  In general, however, they are dependent.
In general, however, they are dependent.
The condition 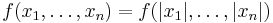 ensures that
ensures that  are of zero mean and uncorrelated; still, they need not be independent, nor even pairwise independent. By the way, pairwise independence cannot replace independence in the classical central limit theorem (Durrett 1996, Section 2.4, Example 4.5).
are of zero mean and uncorrelated; still, they need not be independent, nor even pairwise independent. By the way, pairwise independence cannot replace independence in the classical central limit theorem (Durrett 1996, Section 2.4, Example 4.5).
Here is a Berry-Esseen type result.
Theorem (Klartag 2008, Theorem 1). Let  satisfy the assumptions of the previous theorem, then
satisfy the assumptions of the previous theorem, then
for all 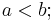 here
here 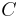 is a universal (absolute) constant. Moreover, for every
is a universal (absolute) constant. Moreover, for every 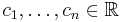 such that
such that 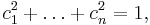
A more general case is treated in (Klartag 2007, Theorem 1.1). The condition 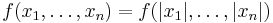 is replaced with much weaker conditions:
is replaced with much weaker conditions: 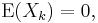
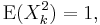
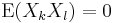 for
for 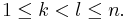 The distribution of
The distribution of 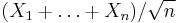 need not be approximately normal (in fact, it can be uniform). However, the distribution of
need not be approximately normal (in fact, it can be uniform). However, the distribution of  is close to N(0,1) (in the total variation distance) for most of vectors
is close to N(0,1) (in the total variation distance) for most of vectors  according to the uniform distribution on the sphere
according to the uniform distribution on the sphere 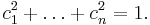
Lacunary trigonometric series
Theorem (Salem - Zygmund). Let U be a random variable distributed uniformly on (0, 2π), and Xk = rk cos(nkU + ak), where
- nk satisfy the lacunarity condition: there exists q > 1 such that nk+1 ≥ qnk for all k,
- rk are such that
- 0 ≤ ak < 2π.
Then
converges in distribution to N(0, 1/2).
See (Zygmund 1959, Sect. XVI.5, Theorem (5-5)) or (Gaposhkin 1966, Theorem 2.1.13).
Gaussian polytopes
Theorem (Barany & Vu 2007, Theorem 1.1). Let A1, ..., An be independent random points on the plane R2 each having the two-dimensional standard normal distribution. Let Kn be the convex hull of these points, and Xn the area of Kn Then
converges in distribution to N(0,1) as n tends to infinity.
The same holds in all dimensions (2, 3, ...).
The polytope Kn is called Gaussian random polytope.
A similar result holds for the number of vertices (of the Gaussian polytope), the number of edges, and in fact, faces of all dimensions (Barany & Vu 2007, Theorem 1.2).
Linear functions of orthogonal matrices
A linear function of a matrix M is a linear combination of its elements (with given coefficients), 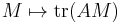 where A is the matrix of the coefficients; see Trace_(linear_algebra)#Inner product.
where A is the matrix of the coefficients; see Trace_(linear_algebra)#Inner product.
A random orthogonal matrix is said to be distributed uniformly, if its distribution is the normalized Haar measure on the orthogonal group O(n,R); see Rotation matrix#Uniform random rotation matrices.
Theorem (Meckes 2008). Let M be a random orthogonal n×n matrix distributed uniformly, and A a fixed n×n matrix such that 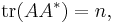 and let
and let 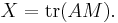 Then the distribution of X is close to N(0,1) in the total variation metric up to
Then the distribution of X is close to N(0,1) in the total variation metric up to 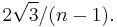
Subsequences
Theorem (Gaposhkin 1966, Sect. 1.5). Let random variables  be such that
be such that 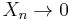 weakly in
weakly in 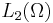 and
and 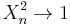 weakly in
weakly in 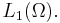 Then there exist integers
Then there exist integers 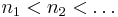 such that
such that 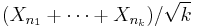 converges in distribution to N(0, 1) as k tends to infinity.
converges in distribution to N(0, 1) as k tends to infinity.
Applications and examples
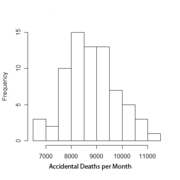
There are a number of useful and interesting examples and applications arising from the central limit theorem (Dinov, Christou & Sanchez 2008). See e.g. [1], presented as part of the SOCR CLT Activity.
- The probability distribution for total distance covered in a random walk (biased or unbiased) will tend toward a normal distribution.
- Flipping a large number of coins will result in a normal distribution for the total number of heads (or equivalently total number of tails).
From another viewpoint, the central limit theorem explains the common appearance of the "Bell Curve" in density estimates applied to real world data. In cases like electronic noise, examination grades, and so on, we can often regard a single measured value as the weighted average of a large number of small effects. Using generalisations of the central limit theorem, we can then see that this would often (though not always) produce a final distribution that is approximately normal.
In general, the more a measurement is like the sum of independent variables with equal influence on the result, the more normality it exhibits. This justifies the common use of this distribution to stand in for the effects of unobserved variables in models like the linear model.
Signal processing
Signals can be smoothed by applying a Gaussian filter, which is just the convolution of a signal with an appropriately scaled Gaussian function. Due to the central limit theorem this smoothing can be approximated by several filter steps that can be computed much faster, like the simple moving average.
The central limit theorem implies that to achieve a Gaussian of variance 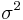
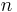 filters with windows of variances
filters with windows of variances  with
with 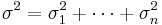 must be applied.
must be applied.
History
Tijms (2004, p. 169) writes:
| “ | The central limit theorem has an interesting history. The first version of this theorem was postulated by the French-born mathematician Abraham de Moivre who, in a remarkable article published in 1733, used the normal distribution to approximate the distribution of the number of heads resulting from many tosses of a fair coin. This finding was far ahead of its time, and was nearly forgotten until the famous French mathematician Pierre-Simon Laplace rescued it from obscurity in his monumental work Théorie Analytique des Probabilités, which was published in 1812. Laplace expanded De Moivre's finding by approximating the binomial distribution with the normal distribution. But as with De Moivre, Laplace's finding received little attention in his own time. It was not until the nineteenth century was at an end that the importance of the central limit theorem was discerned, when, in 1901, Russian mathematician Aleksandr Lyapunov defined it in general terms and proved precisely how it worked mathematically. Nowadays, the central limit theorem is considered to be the unofficial sovereign of probability theory. | ” |
Sir Francis Galton (Natural Inheritance, 1889) described the Central Limit Theorem as:
| “ | I know of scarcely anything so apt to impress the imagination as the wonderful form of cosmic order expressed by the "Law of Frequency of Error". The law would have been personified by the Greeks and deified, if they had known of it. It reigns with serenity and in complete self-effacement, amidst the wildest confusion. The huger the mob, and the greater the apparent anarchy, the more perfect is its sway. It is the supreme law of Unreason. Whenever a large sample of chaotic elements are taken in hand and marshaled in the order of their magnitude, an unsuspected and most beautiful form of regularity proves to have been latent all along. | ” |
The actual term "central limit theorem" (in German: "zentraler Grenzwertsatz") was first used by George Pólya in 1920 in the title of a paper.[7](Le Cam 1986) Pólya referred to the theorem as "central" due to its importance in probability theory. According to Le Cam, the French school of probability interprets the word central in the sense that "it describes the behaviour of the centre of the distribution as opposed to its tails" (Le Cam 1986). The abstract of the paper On the central limit theorem of calculus of probability and the problem of moments by Pólya in 1920 translates as follows.
| “ | The occurrence of the Gaussian probability density 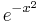 in repeated experiments, in errors of measurements, which result in the combination of very many and very small elementary errors, in diffusion processes etc., can be explained, as is well-known, by the very same limit theorem, which plays a central role in the calculus of probability. The actual discoverer of this limit theorem is to be named Laplace; it is likely that its rigorous proof was first given by Tschebyscheff and its sharpest formulation can be found, as far as I am aware of, in an article by Liapounoff. [...] in repeated experiments, in errors of measurements, which result in the combination of very many and very small elementary errors, in diffusion processes etc., can be explained, as is well-known, by the very same limit theorem, which plays a central role in the calculus of probability. The actual discoverer of this limit theorem is to be named Laplace; it is likely that its rigorous proof was first given by Tschebyscheff and its sharpest formulation can be found, as far as I am aware of, in an article by Liapounoff. [...] |
” |
A thorough account of the theorem's history, detailing Laplace's foundational work, as well as Cauchy's, Bessel's and Poisson's contributions, is provided by Hald.[8] Two historic accounts, one covering the development from Laplace to Cauchy, the second the contributions by von Mises, Pólya, Lindeberg, Lévy, and Cramér during the 1920s, are given by Hans Fischer.[9] A period around 1935 is described in (Le Cam 1986). See Bernstein (1945) for a historical discussion focusing on the work of Pafnuty Chebyshev and his students Andrey Markov and Aleksandr Lyapunov that led to the first proofs of the CLT in a general setting.
A curious footnote to the history of the Central Limit Theorem is that a proof of a result similar to the 1922 Lindeberg CLT was the subject of Alan Turing's 1934 Fellowship Dissertation for King's College at the University of Cambridge. Only after submitting the work did Turing learn it had already been proved. Consequently, Turing's dissertation was never published.[10][11]
See also
- Diversification (finance)
- Illustration of the central limit theorem
- Law of large numbers – weaker conclusion in the same context
- Log-normal distribution – what we get when we multiply random variables in a similar context to the Central limit theorem
- Berry–Esseen theorem – error bounds on normal approximations based on the central limit theorem
- Theorem of de Moivre–Laplace
Notes
- ↑ Johannes Voit (2003), The Statistical Mechanics of Financial Markets (Texts and Monographs in Physics), Springer-Verlag, p. 124, ISBN 3-540-00978-7
- ↑ Theorem 5.3.4, p. 47, A first look at rigorous probability theory, Jeffrey Seth Rosenthal, World Scientific, 2000, ISBN 9810243227.
- ↑ p. 88, Information theory and the central limit theorem, Oliver Thomas Johnson, Imperial College Press, 2004, ISBN 1860944736.
- ↑ pp. 61–62, Chance and stability: stable distributions and their applications, Vladimir V. Uchaikin and V. M. Zolotarev, VSP, 1999, ISBN 9067643017.
- ↑ Theorem 1.1, p. 8, Limit theorems for functionals of random walks, A. N. Borodin, Il'dar Abdulovich Ibragimov, and V. N. Sudakov, AMS Bookstore, 1995, ISBN 0821804383.
- ↑ Marasinghe, M., Meeker, W., Cook, D. & Shin, T.S.(1994 August), "Using graphics and simulation to teach statistical concepts", Paper presented at the Annual meeting of the American Statistician Association, Toronto, Canada.
- ↑ Pólya, George (1920), "Über den zentralen Grenzwertsatz der Wahrscheinlichkeitsrechnung und das Momentenproblem" (in German), Mathematische Zeitschrift 8: 171–181, doi:10.1007/BF01206525, http://www-gdz.sub.uni-goettingen.de/cgi-bin/digbib.cgi?PPN266833020_0008
- ↑ Andreas Hald, History of Mathematical Statistics from 1750 to 1930, Ch.17.
- ↑ Hans Fischer: (1) "The Central Limit Theorem from Laplace to Cauchy: Changes in Stochastic Objectives and in Analytical Methods"; (2) "The Central Limit Theorem in the Twenties".
- ↑ See Hodges's biography of Turing, pp. 87-88.
- ↑ pp. 199 ff., Symmetry and its discontents: essays on the history of inductive probability, S. L. Zabell, Cambridge University Press, 2005, ISBN 0521444705.
References
- Henk Tijms, Understanding Probability: Chance Rules in Everyday Life, Cambridge: Cambridge University Press, 2004.
- S. Artstein, K. Ball, F. Barthe and A. Naor (2004), "Solution of Shannon's Problem on the Monotonicity of Entropy", Journal of the American Mathematical Society 17, 975–982. Also author's site.
- S.N.Bernstein, On the work of P.L.Chebyshev in Probability Theory, Nauchnoe Nasledie P.L.Chebysheva. Vypusk Pervyi: Matematika. (Russian) [The Scientific Legacy of P. L. Chebyshev. First Part: Mathematics] Edited by S. N. Bernstein.] Academiya Nauk SSSR, Moscow-Leningrad, 1945. 174 pp.
- G. Rempala and J. Wesolowski, "Asymptotics of products of sums and U-statistics", Electronic Communications in Probability, vol. 7, pp. 47–54, 2002.
- Dinov, Ivo; Christou, Nicolas; Sanchez, Juana (2008), "Central Limit Theorem: New SOCR Applet and Demonstration Activity", Journal of Statistics Education (ASA) 16 (2). Also at ASA/JSE.
- Billingsley, Patrick (1995), Probability and Measure (Third ed.), John Wiley & sons, ISBN 0-471-00710-2
- Rice, John (1995), Mathematical Statistics and Data Analysis (Second ed.), Duxbury Press, ISBN 0-534-20934-3
- Durrett, Richard (1996), Probability: theory and examples (Second ed.)
- Klartag, Bo'az (2007), "A central limit theorem for convex sets", Inventiones Mathematicae 168, 91–131. Also arXiv.
- Klartag, Bo'az (2008), "A Berry-Esseen type inequality for convex bodies with an unconditional basis", Probability Theory and Related Fields. Also arXiv.
- Le Cam, Lucien (1986), "The central limit theorem around 1935", Statistical Science 1:1, 78–91.
- Zygmund, Antoni (1959), Trigonometric series, II, Cambridge.
- Barany, Imre; Vu, Van (2007), "Central limit theorems for Gaussian polytopes", The Annals of Probability (Institute of Mathematical Statistics) 35 (4): 1593–1621, doi:10.1214/009117906000000791. Also arXiv.
- Meckes, Elizabeth (2008), "Linear functions on the classical matrix groups", Transactions of the American Mathematical Society 360: 5355–5366, doi:10.1090/S0002-9947-08-04444-9. Also arXiv.
- Gaposhkin, V.F. (1966), "Lacunary series and independent functions", Russian Math. Surveys 21 (6): 1–82, doi:10.1070/RM1966v021n06ABEH001196.
- Bradley, Richard (2007), Introduction to Strong Mixing Conditions (First ed.), Heber City, UT: Kendrick Press, ISBN 097404279X
External links
- Animated examples of the CLT
- Central Limit Theorem interactive simulation to experiment with various parameters
- CLT in NetLogo (Connected Probability - ProbLab) interactive simulation w/ a variety of modifiable parameters
- General Central Limit Theorem Activity & corresponding SOCR CLT Applet (Select the Sampling Distribution CLT Experiment from the drop-down list of SOCR Experiments)
- Generate sampling distributions in Excel Specify arbitrary population, sample size, and sample statistic.
- [2] Another proof.
- CAUSEweb.org is a site with many resources for teaching statistics including the Central Limit Theorem
- The Central Limit Theorem by Chris Boucher, Wolfram Demonstrations Project.
- Weisstein, Eric W., "Central Limit Theorem" from MathWorld.
- Animations for the Central Limit Theorem by Yihui Xie using the R package animation
- A visualization of the Central Limit Theorem from Portfolio Monkey.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
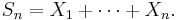
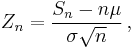
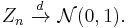
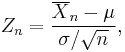
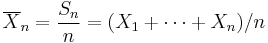
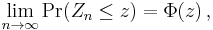
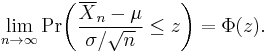
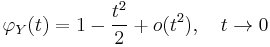
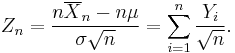
![\left[\varphi_Y\left({t \over \sqrt{n}}\right)\right]^n = \left[ 1 - {t^2
\over 2n} + o\left({t^2 \over n}\right) \right]^n \, \rightarrow \, e^{-t^2/2}, \quad n \rightarrow \infty.](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/5147da59182098ae4ee80d225aa23ed5.png)
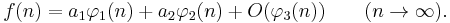
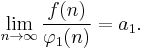
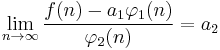
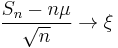
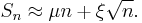
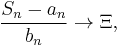
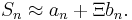
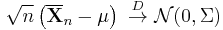
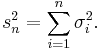
![\lim_{n\to\infty} \frac{1}{s_{n}^{2+\delta}} \sum_{i=1}^{n} \mathbb{E}\left[|X_{i} - \mu_{i}|^{2+\delta}\right] = 0](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/3f42bbfbaac48dfd5798e8c6a683f71f.png)
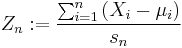
![\lim_{n \to \infty} \frac{1}{s_n^2}\sum_{i = 1}^{n} \operatorname{E}\big[
(X_i - \mu_i)^2 \cdot \mathbf{1}_{\{ | X_i - \mu_i | > \varepsilon s_n \}}
\big] = 0](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/b7d6b08a74420b151e2626ed8d8fb00b.png)